関数

最初は数学で現れるような関数について述べよう. $\sin$ や $\log$のような関数は math モジュールで用意されているが, そうでない場合は, 自分で関数を用意することもできる.

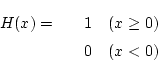
関数は,

def 関数名(引数):
    関数本体

の形式で定義される. (関数 y=f(x) の x を引数と呼んでいる.) いろいろな x の値に対して y=f(x) の値を計算するのである. なお, この定義は, その関数を使用する前に, 行われていなくてはならない.

簡単な例として, ヘビサイド関数を定義してみよう. ヘビサイド関数は

$$\begin{eqnarray*}H(x) = &&1 \quad (x \ge 0) \\ && 0 \quad (x < 0) \end{eqnarray*}$$

なる関数である. 以下の例は, 最初の 5 行が関数 heaviside() の定義で, 後の部分はその関数を呼び出している.

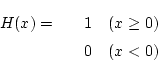
>>> def heaviside(x):
...     if x >= 0:
...         return 1.0
...     else:
...         return 0.0
... 
>>> heaviside(10)
1.0
>>> heaviside(0)
1.0
>>> heaviside(-2)
0.0

関数名に使える文字等は, 変数名の場合と同じである. (もちろん引数は変数の 一種なので, 引数の名前に使える文字等は変数名の場合と一緒である.) また, 同じ名前を別の関数や変数の名前に重複して用いてはならない. なお, return はその後の数値(等)を返し, その関数を終了する.

関数の引数名は, その関数の中でのみ意味を持つ. 関数の外で 同じ名前の変数を別に用いても構わない:

>>> def heaviside(x):
...     if x >= 0:
...         return 1.0
...     else:
...         return 0.0
... 
>>> x = 10
>>> heaviside(x)
1.0

数学でよく出て来る関数は, 引数の取り得る範囲が実数であるが, プログラムでは引数が整数や自然数の範囲のものもよく出て来る. セクション 4.10 で扱った例をもとに, 自然数 n に対して, $1^2 + \dots + n^2$ の値を返す関数 を作ってみよう:

>>> def sqsum(n):
...    sum = 0
...    for i in range(n):
...       sum = sum + (i + 1)**2
...    return sum
... 
>>> sqsum(1)
1
>>> sqsum(10)
385

この関数は n が自然数であることを前提として作られている. (今の場合, それ以外の n に対しては, 関数 range() の仕様に応じた値が返って来て, エラーにはならない.)

関数の引数は, 複数の数値であってもよい. ふたつの数の相乗平均を 返す関数を見てみよう:

>>> def mean2(a, b):
...     return math.sqrt(a * b)
... 
>>> mean2(1,4)
2.0

なお, この例では, math.sqrt() 関数を使っているので, あらかじめ math モジュールを import しておかなくてはならない.

関数の引数は, リストであっても構わない. 以下の関数は, リスト(項目は数値)を引数とし, リストの数値の平均を 返す関数である:

>>> def mean(list_of_num):
...     sum = 0.0
...     for i in list_of_num:
...         sum = sum + i
...     return sum / len(list_of_num)
... 
>>> mean([1, 2, 3])
2.0
>>> list = [1, 3, 5, 7]
>>> mean(list)
4.0
>>> i = [-1, 1, 2]
>>> mean(i)
0.666666666667

上の例では, 関数の中で変数 i を用いて, かつ関数の外でも変数 i を用いてい る. 関数の中で用いている変数(上の例では sum もそうである)は, その関数 の中でのみ意味を持ち, 関数の外で同じ名前の変数を用いても, 異なるものと して扱われる. つまり, 関数を利用する際には, 関数の内部でどのような名前の 変数が使われているかを気にしなくてもよい.

さて, 値を返さない関数(手続きと言うべきだろうか)も, 同様に定義できる. 以下の関数は, 「Hello world.」と印字するだけで, 値は返さない:

>>> def say_hello():
...     print 'Hello world.'
... 
>>> say_hello()
Hello world.
>>> say_hello
<function say_hello at 80c8ee0>

この関数は, 引数もないので, ()の中は空になっている. このような 関数を呼び出すときでも「()」をつけなくてはならないことが, 最後の実行 例からわかる.

最後に注意として, 関数の引数を関数の中で変更した場合にどうなるかを 注意しておこう.

結論(の一部)を言うと, 引数が数値の場合は, 関数の 中で引数を変更しても影響はない. 以下の例で分かるであろう:

>>> def twice(a):
...     a = a * 2
...     return a
... 
>>> a = 10
>>> twice(a)
20
>>> a
10

しかし, リストを引数とした場合には, ある種の操作は, 関数を 呼び出した後に, 引数にしたリストを変更する. 例えば, 次の例を, 上の例と比較してみよ. (list.append(1)は, list の最後に 1 という項目を追加する.)

>>> def plusone(list):
...     list.append(1) # list を変更
... 
>>> list = [1, 2]
>>> plusone(list)
>>> list
[1, 2, 1]

なお, 引数がリストの場合でも, その変更が, 同じ変数名のリストに 新たに代入をしなおすタイプであれば, その関数を呼び出しても, 引数に用いたリストは変更されない:

>>> def plusone2(list):
...     list = list + [1] # list に新たに代入
... 
>>> list = [1, 2]
>>> plusone2(list)
>>> list
[1, 2]

ここでは, これらについて深く追求することはしない. 現段階では, 関数の中で引数の内容を変更することは避けたほうが無難であろう.

ある種の計算では, 関数を用いてリストを変更したくなることもあるであろうが, Python は関数でリストを返すことも出来るので, 変更したリストを返すような 関数を作成すればよい. 例えば, リストの全ての項目(各項目は数)を 2 倍した いときには, 以下のようにすることもできる:

>>> def twice_list(list):
...     tmp = [] # 空のリスト. こちらに結果を入れる.
...     for i in list:
...         tmp = tmp + [2 * i] # 各項目を 2 倍したものを最後につける.
...     return tmp
... 
>>> twice_list([1, 2, 3])
[2, 4, 6]

参考のため, 引数にしたリストを変更するタイプの例もあげておこう:

>>> def twice_list2(list):
...     for i in range(len(list)):
...         list[i] = list[i] * 2
... 
>>> a = [1, 2]
>>> twice_list2(a)
>>> a
[2, 4]

いずれにせよ, 作成したプログラムがどのように動作するかは, 慎重に チェックしておく必要がある.